1. 离散型
1.1 Z=X+Y 型
定义:设 (X,Y) 为二维离散型随机变量,X 与 Y 独立,Z=X+Y,则 Z 的分布律为
P(Z=zk)=i=1∑∞P(X=xi,Y=zk−xi)
此公式也可称为离散卷积公式

1.2 一般方法

2. 连续型
2.1 Z=X+Y 型
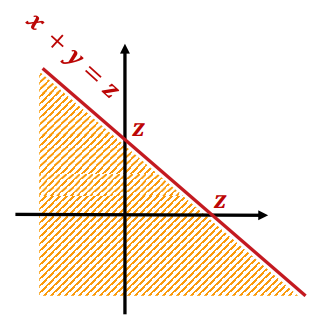
2.1.1 一般情况
对于连续情形,Z 的概率密度函数为 fZ(z)=∫−∞∞fX,Y(x,z−x)dx
==特别的==,若 X 和 Y 相互独立,该公式也可以写作
fZ(z)=∫−∞∞fX(x)fY(z−x)dx=fX(z)∗fY(z)
此公式也称为卷积公式
2.1.2 推广
已知 (X,Y) 的联合密度 f(x,y),求 Z=aX+bY+c 的概率密度,其中 a,b,c 为常数。且 a,b=0
则
fZ(z)=∣b∣1∫−∞∞f(x,bz−ax−c)dx=∣b∣1f(x,bz−c)∗fX(x)
2.1.3 正态随机变量的结论
若 (X,Y)∼N(μ1,μ2,σ12,σ22,ρ),则 X+Y∼N(μ1+μ2,σ12+σ22+2ρσ1σ2)
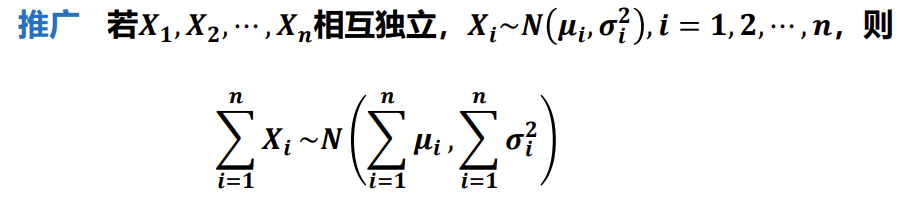
2.2 Z=X/Y 型
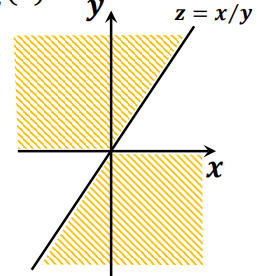
2.2.1 一般情况
对于 Z=YX ,有
fZ(z)=∫−∞∞∣y∣f(yz,y)dy
若 X 和 Y 相互独立,则
fZ(z)=∫−∞∞fX(yz)fY(y)∣y∣dy
2.3 Z=X2+Y2 型
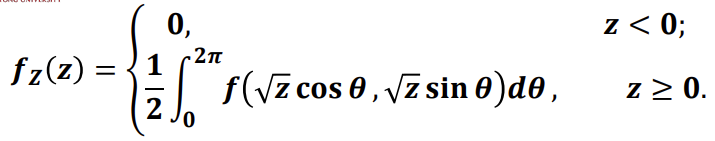
2.4 极值分布

